Vertex Form of a Parabola

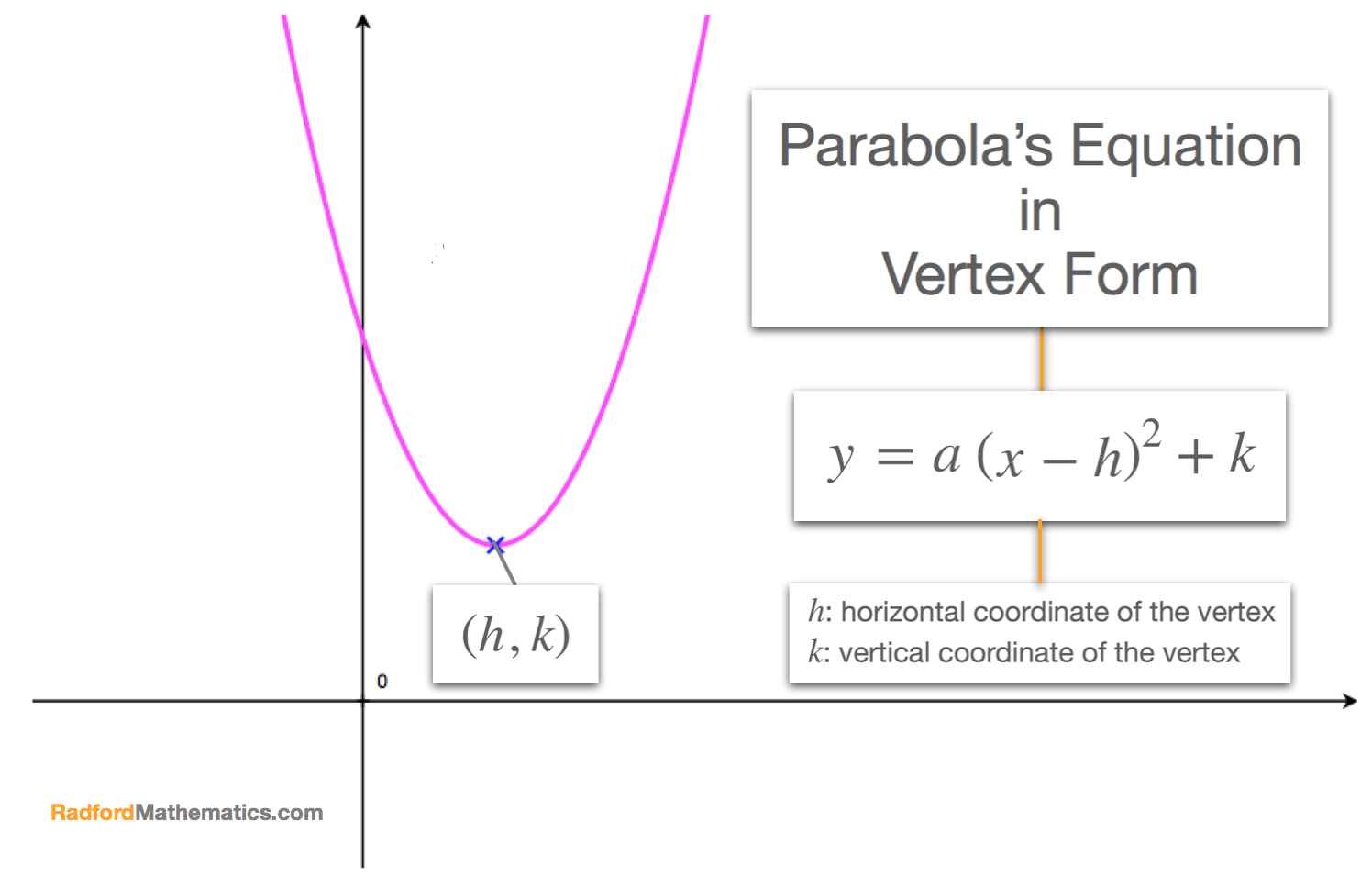
In the previous section, we learnt how to write a parabola in its vertex form and saw that a parabola's equation: \[y = ax^2+bx+c\] could be re-written in vertex form: \[y = a\beginx - h \end^2+k\] where:

• \(h\): is the horizontal coordinate of the vertex
• \(k\): is the vertical coordinate of the vertex.

We can use the vertex form to find a parabola's equation. The idea is to use the coordinates of its vertex (maximum point, or minimum point) to write its equation in the form \(y=a\beginx-h\end^2+k\) (assuming we can read the coordinates \(\beginh,k\end\) from the graph) and then to find the value of the coefficient \(a\).

This is explained in the step-by-stem mathod, below, as well as in the tutorials.

How to find a parabola's equation using its Vertex Form

Given the graph of a parabola for which we're given, or can clearly see:

• the coordinates of the vertex, \(\beginh,k\end\), and:
• the coordinates another point \(P\) through which the parabola passes.

• Step 1: use the (known) coordinates of the vertex, \(\beginh,k\end\), to write the parabola's equation in the form: \[y = a\beginx-h \end^2+k\] the problem now only consists of having to find the value of the coefficient \(a\).
• Step 2: find the value of the coefficient \(a\) by substituting the coordinates of point \(P\) into the equation written in step 1 and solving for \(a\).

This two-step method is better/further explained in the following tutorial, take the time to watch it now.

Tutorial 1

In the following tutorial we learn how to find a parabola's using the coordinates of its vertex as well as the coordinates of its \(y\)-intercept.

Your browser does not support the video tag.

Exercise 1

Using the two-step method we've just learned, find the equation of each of the following parabola in the following two forms:

1. \(y=a\beginx-h\end^2+k\)
2. \(y = ax^2+bx+c\)

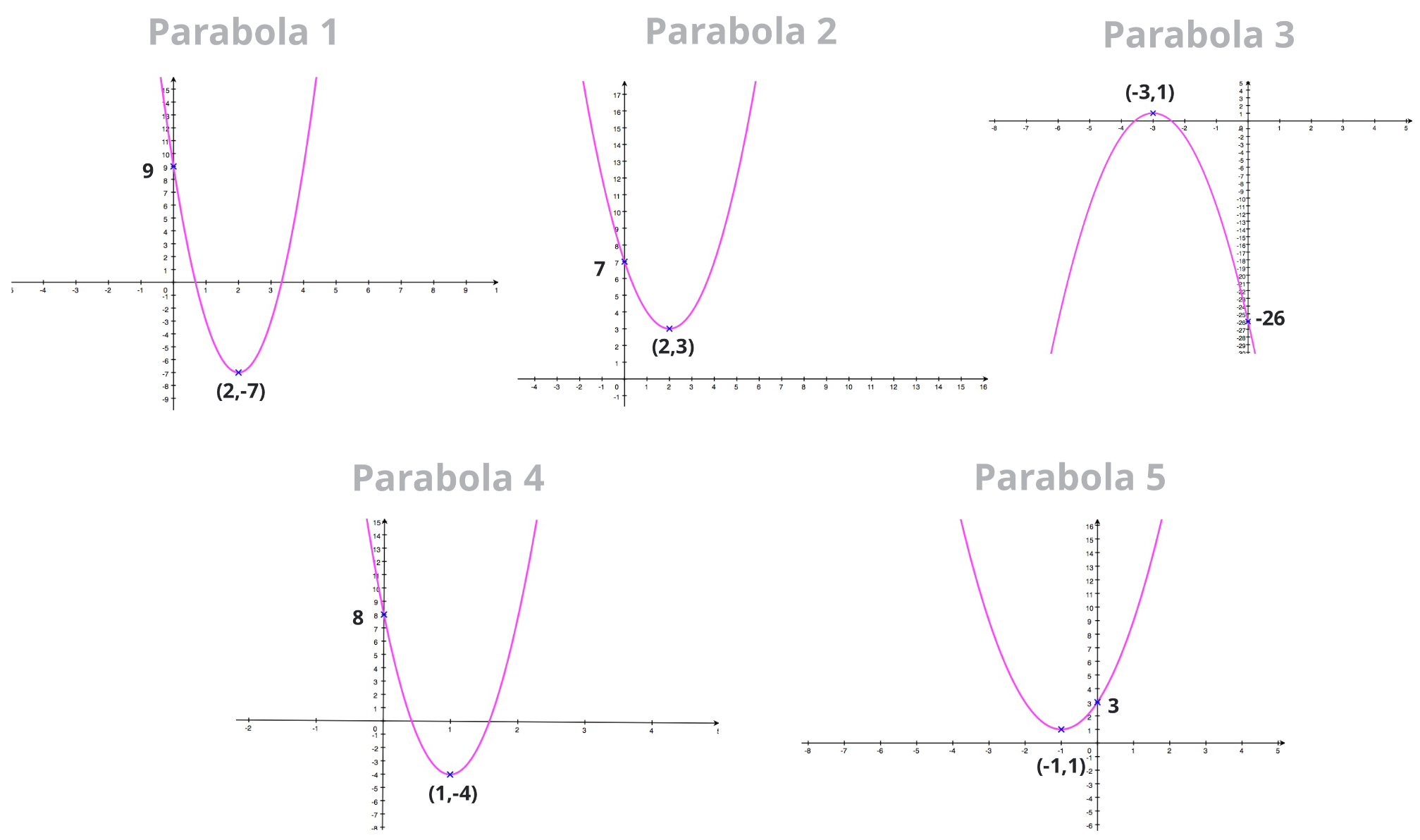
Note: this exercise can be downloaded as a worksheet to practice with worksheet

Answers Without Working

• Parabola 1:
  1. \(y = 4 \beginx-2\end^2-7\)
  2. \(y = 4x^2 - 16x + 9\)
• Parabola 2:
  1. \(y = \beginx-2\end^2+ 3\)
  2. \(y = x^2 - 4x +7\)
• Parabola 3:
  1. \(y = -3 \beginx+3 \end^2+1\)
  2. \(y=-3x^2 - 18x - 26\)
• Parabola 4:
  1. \(y = 12 \beginx-1\end^2-4\)
  2. \(y = 12x^2 - 24x + 8\)
• Parabola 5:
  1. \(y = 2\beginx+1 \end^2+1\)
  2. \(y = 2x^2+4x+3\)

Answers with Working

Select the question number you'd like to see the working for: